学习笔记11 分钟 读完 (大约 1645 个字)

「多项式学习笔记Part I」最基本的多项式乘法

最近正好月考，然而并不想去月考，于是来颓 blog 吧。

给你一个 $n-1$ 次多项式 $F(x)$ 和一个 $m-1$ 次多项式 $G(x)$，让你求 $(F\times G)(x)$ 的各项系数。$n,m\leqslant 10^{6}$。

我们不妨将 $F(x)$ 的 $i$ 次项系数记为 $F[i]$

不难发现直接暴力算是 $O(n^{2})$ 的，因此我们需要优化。

不过为了优化，我们得先扯远点。

点值表达

如果我们选取 $n$ 个点 $(x_{0},y_{0}),(x_{1},y_{1}),\cdots,(x_{n-1},y_{n-1})$，并且其中 $x_{i}$ 两两不同，我们就可以唯一地确定出一个 $n-1$ 次多项式。

就比如说

瞎写的（

我们可以列出如下的三元一次方程组：

解得

注意到 $(F\times G)(x)=F(x)G(x)$（废话），我们只要知道了 $F(x)$ 和 $G(x)$ 的点值表达，就可以 $O(n)$ 的计算出 $(F\times G)(x)$ 的点值表达了。因为 $(F\times G)(x)$ 的次数是 $n+m-2$，我们选出前 $n+m-1$ 个自然数即可。

但是这还不够。注意到，如果我们选取的点的横坐标如果很普通，我们首先需要 $O(n^{2})$ 转成点值表达，乘完之后又要转回系数表达，效率甚至不如暴力（

于是我们还需要优化，于是我们还需要再扯远一点。

复数

对，你没看错，扯到复数了。

基本概念

根据初中学习的数学知识，我们知道有些一元二次方程是没有实数根的。就比如说

我们知道，它的判别式是 $\Delta=b^{2}-4ac=-4\lt 0$，因此它没有实数根。

于是我们就定义了虚数单位 $i$，并规定 $i^{2}=-1$。形如 $x+yi$ 这样的数被称为复数。它的模长被定义为它到原点的距离，即 $\sqrt{x^{2}+y^{2}}$；幅角被定义为与 $x$ 轴正半轴的夹角，即 $\operatorname{tan}^{-1}\cfrac{y}{x}$。

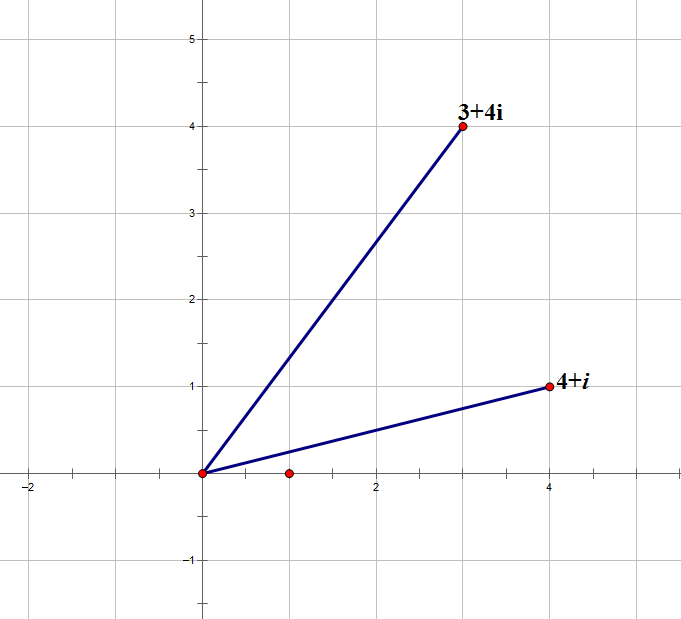
因为 $i$ 不是实数，它不能被画在我们现有的数轴上。那我们就再拿来一条数轴，将两条数轴垂直放置，垂足为原点。或者说，我们可以将这理解成平面直角坐标系，$x$ 就是实轴，$y$ 轴就是虚轴，$x+yi$ 就对应了点 $(x,y)$。

上图展示了 $4+i$ 和 $3+4i$。

复数的运算其实没什么出乎意料的：

我们来单独考虑一下复数相乘的几何意义。

假设我们有两个复数 $c_{1}$，$c_{2}$，它们的模长分别是 $r_{1}$，$r_{2}$，幅角分别是 $\alpha_{1}$，$\alpha_{2}$。不难发现我们有

总结成一句话，就是「模长相乘，幅角相加」。

单位圆与单位根

单位圆就是指半径为 $1$ 的圆。不过一般我们都是把它画在原点的。

考虑这么一个方程

它的所有复数根。

因为复数相乘意味着模长相乘，如果一个复数的 $n$ 次方等于 $1$，它自身的模长也应该是 $1$。如果它的幅角是 $a$，我们应该有

不难想象出我们有 $n$ 个这样的复数，它们的幅角通式是 $\cfrac{2k\pi}{n}(k\in[0,n)\cap\mathbb{Z})$。我们称其中幅角等于 $\cfrac{2\pi}{n}$ 的复数，即 $\cos\cfrac{2\pi}{n}+i\sin\cfrac{2\pi}{n}$ 为 $n$ 次单位根 $\omega_{n}$，我们就可以把这 $n$ 个复数表示为 $\omega_{n}^{k}(k\in[0,n)\cap\mathbb{Z})$。

它有如下的一些性质

因为它们的模长都是 $1$，幅角相等就相等了。

然后就没了，读者自证不难（

因为 $\omega_{n}^{\frac{n}{2}}$ 的幅角是 $\cfrac{2\times\frac{n}{2}\pi}{n}=\pi$，不难发现它就是 $-1$ 了。

快速傅里叶变换（Fast Fourier Transformation）

运行过程

那么问题来了，我们刚才扯了这么些，有什么用呢？

就是说，有个叫「让 · 巴普蒂斯 · 约瑟夫 · 傅里叶」（Jean Baptiste Joseph Fourier）的神仙有一天大开脑洞，掏出 $n$ 次单位根想要求点值表达。

首先，我们通过在高次补 $0$ 的方式，将这个多项式的项数（也就是次数 $+1$）补到 $2$ 的非负整数次幂。

然后一巴掌把这个多项式拍成两半，按奇偶性拼成两个多项式：

于是我们有

现在我们假设 $0\leqslant k<\cfrac{n}{2}$，将 $x=\omega_{n}^{k}$ 和 $x=\omega_{n}^{k+\frac{n}{2}}$ 代入

我们注意到，如果说我们求出了 $F_{1}(x)$ 和 $F_{2}(x)$ 的点值表达，我们就能够 $O(n)$ 地求出 $F(x)$ 的点值表达了。至此，我们不难想到分治，边界条件就是 $n=1$，这时什么也不用做直接返回即可。

简单地贴一下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void work(complex* F,int n){
     if(n==1)
         return;
     complex F1[n>>1],F2[n>>1];
 for(int i=0;i<n;i+=2){
 	 F1[i]=F[2*i];
 F2[i]=F[2*i+1];
     }
 work(F1,n>>1);
 work(F2,n>>1);
 complex unit(cos(2*Pi/n),sin(2*Pi/n)),tmp=1;
 for(int i=0;i<(n>>1);++i,tmp=tmp*unit){
 	 complex w=F2[i+(n>>1)]*tmp;
 F[i]=F1[i]+w;
 F[i+(n>>1)]=F1[i]-w;
     }
}

不过，以上代码是我现写出来的，保证其不正确性不保证其正确性。

不过，这样递归运算效率还是太低了。我们来考虑一下，递归到底层后，F 数组的每一个位置上实际存的是几次项：

1
2
3
4
0 1 2 3 4 5 6 7
0 2 4 6|1 3 5 7
0 4|2 6|1 5|3 7
0|4|2|6|1|5|3|7

写成二进制看看：

位置（十进制） 位置（二进制） 次数（十进制） 次数（二进制）
$0$ $000$ $0$ $000$
$1$ $001$ $4$ $100$
$2$ $010$ $2$ $010$
$3$ $011$ $6$ $110$
$4$ $100$ $1$ $001$
$5$ $101$ $5$ $101$
$6$ $110$ $3$ $011$
$7$ $111$ $7$ $111$

注意到两边的数字的二进制是镜像的。也就是说，我们只要把位置编号的二进制位的最后 $\operatorname{log}n$ 位左右镜像过来，就可以得到递归到最底层后，这个位置上的系数所对应的项的次数了。

我们可以 $O(n)$ 地处理处每个数的镜像：

1
2
for(int i=0;i<n;++i)
     rev[i]=(rev[i>>1]>>1)|((i&1)?(n>>1):0);

中间有一个位或运算符，我们以它为分界线，将上面这行代码分成左右两部分。左边就是 $i$ 这个数除了最后一位以外的所有位的镜像；右边特判了一下 $i$ 的最后一位是否为 $1$，如果是的话，就在最高位补一个 $1$。

接下来的步骤我不是很能解释得清楚，因为我也是背的板子。总之这个东西写出来差不多长这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void work(complex* F,int n){
     for(int i=0;i<n;++i)
         if(i<rev[i])
             swap(F[i],F[rev[i]]);
     for(int len=2,p=1;len<=n;len<<=1,p<<=1){
         complex unit(cos(Pi/p),sin(Pi/p));
         for(int i=0;i<n;i+=len){
             complex cur(1,0);
             for(int j=i;j<i+p;++j){
                 complex tmp=F[j+p]*cur;
                 F[j+p]=F[j]-tmp;
                 F[j]=F[j]+tmp;
                 cur=cur*unit;
             }
         }
     }
}

那么现在还差最后一步，将点值表达转回系数表达。我们将 $F(\omega_{n}^{0}),F(\omega_{n}^{1}),\cdots,F(\omega_{n}^{n-1})$ 分别记为 $y_{0},y_{1},\cdots,y_{n-1}$，我们求点值的过程可以用矩阵表达成这样：

我们可以试图寻找左边那个矩阵的逆矩阵。直接摆结论的话，它差不多长这样：

现在我们要证明这两个矩阵乘起来是单位矩阵。令第一个矩阵为 $A$，第二个矩阵为 $B$，$A\times B=C$。不难发现 $A[i][j]=\omega_{n}^{ij}$，$B[i][j]=\cfrac{1}{n}\omega_{n}^{-ij}$，我们有

若 $i=j$，不难发现此时 $C[i][j]=1$。

否则，即 $i\neq j$，设 $i-j=l$，我们有

综上所述，矩阵 $C$ 是单位矩阵，因此矩阵 $B$ 是矩阵 $A$ 的逆矩阵。

因此我们有

注意到这个过程和我们之前将系数转化为点值表达的过程极为相似。这就是在启示我们，如果说我们把之前用的 $\omega_{n}^{0},\omega_{n}^{1},\cdots,\omega_{n}^{n-1}$ 换成 $\omega_{n}^{0},\omega_{n}^{-1},\cdots,\omega_{n}^{-n+1}$，然后对着点值表达来一遍 FFT，然后再除以 $n$，就得到了原多项式的系数了。

注意到这两个过程只有用到的单位根不一样，我们可以将上面那段代码的

1
complex unit(cos(Pi/p),sin(Pi/p));

改成

1
complex unit(cos(Pi/p),tp*sin(Pi/p));

然后调用时再传一个参数 tp 进去。tp=1 表示是系数转点值，tp=-1 表示是点值转系数。

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<cstdio>
#include<cmath>
#define maxn 2097152

const double Pi=acos(-1.0);

int n,m;
int rev[maxn+1];
struct complex{
     double r,c;

     complex(double _r=0,double _c=0){
         r=_r;
         c=_c;
     }
};
complex F[maxn+1],G[maxn+1];

inline complex operator+(complex& a,complex& b){
     return complex(a.r+b.r,a.c+b.c);
}

inline complex operator-(complex& a,complex& b){
     return complex(a.r-b.r,a.c-b.c);
}

inline complex operator*(complex& a,complex& b){
     return complex(a.r*b.r-a.c*b.c,a.r*b.c+a.c*b.r);
}

template<typename _tp>
inline void swap(_tp& x,_tp& y){
    _tp tmp=x;
     x=y;
     y=tmp;
}

inline void FAQ(complex F[],int tp){
     for(register int i=0;i<n;++i)
         if(i<rev[i])
             swap(F[i],F[rev[i]]);
     for(register int len=2,p=1;len<=n;len<<=1,p<<=1){
         register complex unit(cos(Pi/p),tp*sin(Pi/p));
         for(register int i=0;i<n;i+=len){
             register complex cur(1,0);
             for(register int j=i;j<i+p;++j){
                 register complex tmp=F[j+p]*cur;
                 F[j+p]=F[j]-tmp;
                 F[j]=F[j]+tmp;
                 cur=cur*unit;
             }
         }
     }
}

int main(){
     scanf("%d%d",&n,&m);
     ++n;
     for(register int i=0;i<n;++i)
         scanf("%d",&F[i].r);
     ++m;
     for(register int i=0;i<m;++i)
         scanf("%d",&G[i].r);
     for(m+=n-1,n=1;n<m;n<<=1);
     for(register int i=0;i<n;++i)
         rev[i]=(rev[i>>1]>>1)|((i&1)?(n>>1):0);
     FAQ(F,1);
     FAQ(G,1);
     for(register int i=0;i<n;++i)
         F[i]=F[i]*G[i];
     FAQ(F,-1);
     for(register int i=0;i<m;++i)
         printf("%0.0lf ",F[i].r/n);
     return 0;
}

不要问我 cltstream 哪去了（

然后您就可以切掉这道板子题 了。

其实上面的代码是我从另一道题里复制过来然后现改的，说不定会改出错（

最好还是自己写吧（

什么？想知道是哪道题？往下看（

例题

「ZJOI2014」力

这是一道裸的卷积题。

考虑两个长度为 $n$ 的数组 $F$ 和 $G$，现在我们想求一个数组 $H$，它满足

在本页面往上翻，翻到这个式子：

发现了吗？这两个过程其实是一样的。

于是，我们如下构造两个多项式

然后直接一波 FFT 套上去，输出次数最低的 $n$ 项的系数就好。

那么这题呢？首先我们把 $j\lt i$ 和 $j\gt i$ 分开计算。

先考虑 $j\lt i$，令 $F[i]=q_{i}$，$G[i]=\begin{cases}&\cfrac{1}{i^{2}}\;\;&(i\gt 0)\\&0&(i=0)\end{cases}$，那么

直接套板子就行。

对于 $j>i$ 的情况，我们将数组 $F$ 左右翻转，然后继续套板子就行（

具体还是看代码吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include\lt cstdio>
#include<cmath>
#define maxn 2097152

const double Pi=acos(-1.0);

int n,m;
int rev[maxn+1];
struct complex{
     double r,c;

     complex(double _r=0,double _c=0){
         r=_r;
         c=_c;
     }
};
complex F1[maxn+1],F2[maxn+1],G[maxn+1];

inline complex operator+(complex& a,complex& b){
     return complex(a.r+b.r,a.c+b.c);
}

inline complex operator-(complex& a,complex& b){
     return complex(a.r-b.r,a.c-b.c);
}

inline complex operator*(complex& a,complex& b){
     return complex(a.r*b.r-a.c*b.c,a.r*b.c+a.c*b.r);
}

template<typename _tp>
inline void swap(_tp& x,_tp& y){
    _tp tmp=x;
     x=y;
     y=tmp;
}

inline void FAQ(complex F[],int tp){
     for(register int i=0;i<n;++i)
         if(i<rev[i])
             swap(F[i],F[rev[i]]);
     for(register int len=2,p=1;len<=n;len<<=1,p<<=1){
         register complex unit(cos(Pi/p),tp*sin(Pi/p));
         for(register int i=0;i<n;i+=len){
             register complex cur(1,0);
             for(register int j=i;j<i+p;++j){
                 register complex tmp=F[j+p]*cur;
                 F[j+p]=F[j]-tmp;
                 F[j]=F[j]+tmp;
                 cur=cur*unit;
             }
         }
     }
}

int main(){
     scanf("%d",&n);
     for(register int i=0;i<n;++i){
         scanf("%lf",&F1[i].r);
         F2[n-i-1].r=F1[i].r;
     }
     for(register int i=1;i<n;++i)
         G[i]=1.0/i/i;
     for(m=n,n=1;n<m;n<<=1);
     n<<=1;
     for(register int i=0;i<n;++i)
         rev[i]=(rev[i>>1]>>1)|((i&1)?(n>>1):0);
     FAQ(G,1);
     FAQ(F1,1);
     for(register int i=0;i<n;++i)
         F1[i]=F1[i]*G[i];
     FAQ(F1,-1);
     FAQ(F2,1);
     for(register int i=0;i<n;++i)
         F2[i]=F2[i]*G[i];
     FAQ(F2,-1);
     for(register int i=0;i<m;++i)
         printf("%lf\n",(F1[i].r-F2[m-i-1].r)/n);
     return 0;
}

数论变换（Number-Theoretic Transformation）

注意到朴素的 FFT 使用的是单位复根。然而它们有一个十分大的缺陷，就是必须要用 double 存。这会带来精度上的误差，一个直接的结果就是，对于只有整数参与的多项式乘法，跑完 FFT 却会出现小数。

这就启示我们，能不能用其他的什么东西替换掉单位复根。

设有两个互质的正整数 $a$ 和 $p$，最小的使得 $a^{k}\equiv 1\pmod{p}$ 的 $k$ 被称为 $a$ 模 $p$ 的阶，记作 $\delta_{p}(a)$。

如果说 $\delta_{p}(a)=\varphi(p)$，我们就称 $a$ 是模 $p$ 的一个原根。

现在我们找一个质数 $p=an+1$，其中 $a$ 是一个正整数，$n$ 是 $2$ 的非负整数次幂。然后我们找到它的原根 $g$，并定义 $\omega_{n}=g^{a}$。让我们来看看单位复根有的性质现在的原根有没有：

$\omega_{n}^{0},\omega_{n}^{1},\cdots,\omega_{n}^{n-1}$ 互不相同。这是为了保证点值表达的合法。

虽然我不会证，不过我们的确有 $g^{0},g^{1},\cdots,g^{n-1}$ 在模 $p$ 意义下互不相同，$a$ 次幂自然也一样。

Updated on 2019-03-17

似乎这么证明有些问题？

原根的这个性质实际上是 $g^{0},g^{1},\cdots,g^{p-2}$ 在模 $p$ 意义下互不相同。因此如果 $(n-1)a<p-1$，那么上面的结论就是正确的。

以上。

$\omega_{2n}^{2k}=\omega_{n}^{k}$。这是为了让我们可以分治。

根据定义，$\omega_{2n}=g^{\frac{a}{2}}$，就是将现在的 $p$ 进一步拆成 $\cfrac{a}{2}\cdot2n+1$。不难发现

因而原根有上述性质。

$\omega_{n}^{k+\frac{n}{2}}=-\omega_{n}^{k}$，或者说 $\omega_{n}^{\frac{n}{2}}=-1$。这同样是为了让我们可以分治。

因为 $p=an+1$，根据费马小定理，我们有

因而 $\omega_{n}^{\frac{n}{2}}\equiv\pm 1\pmod{p}$。又因为 $\omega_{n}^{0}=1$，而 $\omega_{n}^{\frac{n}{2}}\not\equiv\omega_{n}^{0}\pmod{p}$，我们就得到 $\omega_{n}^{\frac{n}{2}}\equiv -1\pmod{p}$。

若 $k\neq 0$，$\sum_{i=0}^{n-1}(\omega_{n}^{k})^{i}=0$。这是为了实现逆变换。不过这个很明显，就留作习题吧。

以上，我们成功地用原根取代了单位复根。一般情况下，我们会取 $p=998244353=7\times 17\times 2^{23}+1$，它的原根是 $3$。

需要注意的是，我们还有一个可以优化的小细节。注意到 $\omega_{n}=g^{a}=g^{\frac{p-1}{n}}$，我们可以将这些值预处理出来，就不用每次都跑快速幂了。对于 $998244353$ 来说，我们需要预处理 $\omega_{2},\omega_{4},\cdots,\omega_{2^{23}}$。注意到

我们一遍快速幂算出 $\omega_{2^{23}}$ 然后倒着推出剩下的即可。

关于 $\omega_{n}^{-k}$，注意到它就是 $\omega_{n}^{k}$ 在模 $998244353$ 意义下的逆元。那么我们把上面两个式子中的 $3$ 换成它在模 $998244353$ 意义下的逆元即可，这个数是 $332748118$。

然后我们把 FFT 板子里的单位复根全部换成原根，运算换成模意义下的就行了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include<cstdio>
#define re register
#define maxn 2097152
#define mod 998244353
#define swap(a,b) a^=b,b^=a,a^=b

namespace cltstream{
     #define size 1048576
     char cltin[size+1],*ih=cltin,*it=cltin;
     inline char gc(){
         #ifdef ONLINE_JUDGE
             if(ih==it){
                 it=(ih=cltin)+fread(cltin,1,size,stdin);
                 if(ih==it)
                     return EOF;
             }
             return *ih++;
         #else
             return getchar();
         #endif
     }

     char cltout[size+1],*oh=cltout,*ot=cltout+size;
     inline void pc(char c){
         if(oh==ot){
             fwrite(cltout,1,size,stdout);
             oh=cltout;
         }
        *oh++=c;
     }
     #define clop() fwrite(cltstream::cltout,1,cltstream::oh-cltstream::cltout,stdout)
     #undef size

     template <typename _tp>
     inline void read(_tp& x){
         int sn=1;
         char c=gc();
         for(;c!=45&&(c<48||c>57)&&c!=EOF;c=gc());
         if(c==45&&c!=EOF)
             sn=-1,c=gc();
         for(x=0;c>=48&&c<=57&&c!=EOF;x=(x<<3)+(x<<1)+(c^48),c=gc());
         x*=sn;
     }

     template <typename _tp>
     inline void write(_tp x,char text=-1){
         if(x<0)
             pc(45),x=-x;
         if(!x)
             pc(48);
         else{
             int digit[22];
             for(digit[0]=0;x;digit[++digit[0]]=x%10,x/=10);
             for(;digit[0];pc(digit[digit[0]--]^48));
         }
         if(text>=0)
             pc(text);
     }
}

int n,m;
int unit[2][24],rev[maxn+1],F[maxn+1],G[maxn+1];

inline int cltpow(re int x,re int y){
     re int res=1;
     for(;y;){
         if(y&1)
             res=1LL*res*x%mod;
         x=1LL*x*x%mod;
         y>>=1;
     }
     return res;
}

inline void NTT(int* F,re int tp){
     for(re int i=0;i<n;++i)
         if(i<rev[i])
             swap(F[i],F[rev[i]]);
     for(re int k=1,p=1;p<n;++k,p<<=1)
         for(re int i=0;i<n;i+=p<<1)
             for(re int j=i,tmp=1;j<i+p;++j,tmp=1LL*tmp*unit[tp][k]%mod){
                 re int x=F[j],y=1LL*F[j+p]*tmp%mod;
                 F[j]=(x+y)%mod;
                 F[j+p]=(x-y+mod)%mod;
             }
}

int main(){
     unit[0][23]=cltpow(3,119);
     unit[1][23]=cltpow(332748118,119);
     for(re int i=0;i<2;++i)
         for(re int j=22;j>=0;--j)
             unit[i][j]=1LL*unit[i][j+1]*unit[i][j+1]%mod;
     cltstream::read(n);
     cltstream::read(m);
     ++n;
     for(re int i=0;i<n;++i)
         cltstream::read(F[i]);
     ++m;
     for(re int i=0;i<m;++i)
         cltstream::read(G[i]);
     for(m+=n-1,n=1;n<m;n<<=1);
     for(re int i=0;i<n;++i)
         rev[i]=(rev[i>>1]>>1)|((i&1)?(n>>1):0);
     NTT(F,0);
     NTT(G,0);
     for(re int i=0;i<n;++i)
         F[i]=1LL*F[i]*G[i]%mod;
     NTT(F,1);
     n=cltpow(n,mod-2);
     for(re int i=0;i<m;++i)
         cltstream::write(1LL*F[i]*n%mod,i<m-1?32:-1);
     clop();
     return 0;
}

以上。

#

评论

关注我

链接

分类

标签

2-SAT1
20091
20121
20141
20161
20171
20181
20192
20201
20222
20233
2D1
AGC1
AHOI1
AtCoder4
BFS 序1
BFS序1
BZOJ1
Boruvka1
Burnside 引理1
CCPC Final1
CodeForces2
Codeforces11
DFS 序1
DFS序1
DP5
Dijkstra2
EC Final1
Epiphany1
FFT2
FWT1
HEOI2
HNOI1
ICPC2
LCT3
Luogu17
MOD1
NOIp1
NTT12
Nono 4431
OEIS1
RPG2
Regional1
Rogue2
SA1
SDOI4
SHU1
STG3
Splay1
TJOI1
Ynoi1
loli1
min_25筛1
yukicoder1
yukicoder contest1
三角函数1
上海1
东方5
二分答案2
交互2
以撒的结合1
伯努利数1
像素风1
公平组合游戏1
其它1
分块5
剧情丰富1
动态规划1
博弈论1
卡牌游戏1
卡特兰数1
原题1
合肥1
同学聚会2
向量1
图论3
块状分块1
多点求值1
多项式3
大学2
失败3
字符串1
容斥2
差分1
希腊神话背景1
平台跳跃1
平衡树2
思维4
成都1
排序1
推理1
提交答案1
数学期望2
数据结构2
数论11
斜率优化1
斯特林数1
施工中1
暴力1
暴力 DP1
最大流1
最小生成树1
最短路1
期望1
杂题13
杜教筛1
构造7
树套树1
树形 DP2
树状数组4
树链剖分1
根号算法1
概率论2
模拟1
模拟赛1
毒瘤2
点分治1
爬山1
状态压缩1
状态压缩 DP1
猫1
猴子1
玄学1
珂朵莉树2
生成函数3
瞪眼1
矩阵3
矩阵乘法1
矩阵快速幂1
离散化1
简单题2
类欧几里得1
线性代数1
线段树4
组合数学4
网络流2
网络赛1
群论1
肉鸽1
肝1
背包1
莫比乌斯反演2
莫队2
虚树2
观察性质1
解谜2
计数1
贪心2
转置原理1
随机游走1
随机算法1
随笔1
难题4
预留推进1
颓废2
题目组1
（广义）音游1

订阅更新

最新文章

归档

×