随笔题解 Pb. 1

前几天《2022 年安徽省机器人大赛本科组》的 K 题，也就是最后一题。

虽然听说都是原题，不过我懒得去找了。

给定一张 $n$ 个节点 $2n-3$ 条边的无向图，保证这些边形成了一个正 $n$ 边形的三角剖分。求这张图的一个最小点覆盖。

$n\leqslant 10^5$。

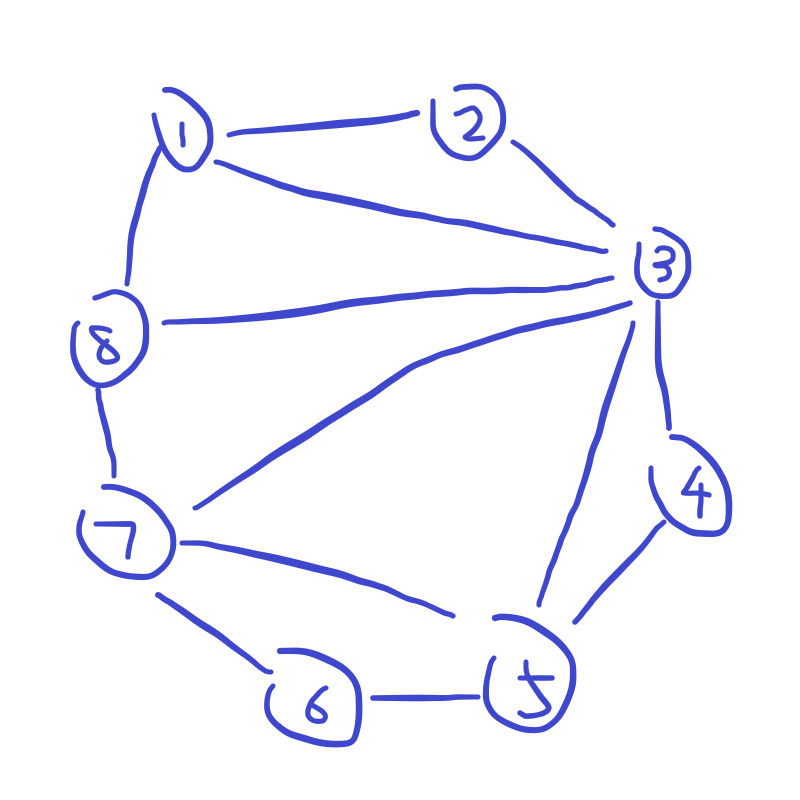
对于上面这个样例来说，答案为 $\{1,3,5,7\}$。

考虑多边形内部的某一个三角形，不难发现这三个节点中，至多有一个不在点覆盖内。

如果确定了某一个节点不在点覆盖内，那么与该节点相邻的所有三角形，它们的其它节点则必须在点覆盖内。

考虑对于每个三角形建立一个方点。

如果两个三角形公用一条边，就在两个对应的方点间连一条边。

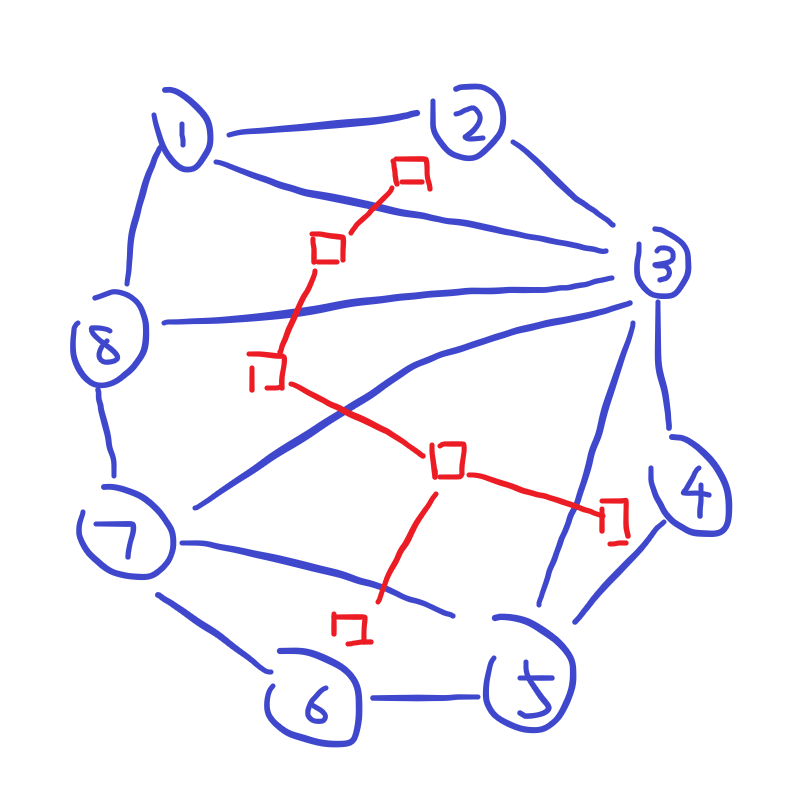
考虑一下这张新图。如果其中出现环，说明多个三角形共用了一个节点，而且这个节点必须要严格在多边形内部才可以。因此新图不存在环。

同时显而易见地，新图是联通的。因此新图是一棵树。

那么下一步，考虑与某个节点相邻的所有三角形，这些三角形对应的方点一定形成了新图中的一条简单路径。

于是问题转化成，给定一棵树和若干条简单路径，选择尽可能多的路径（对应原图中选择尽可能多的点不在点覆盖内），使得这些被选择的路径互不相交（对应点覆盖的性质）。

这应该是一道树上 DP，但是我调不出来了 :(

读者可自行尝试（光速逃